Konsep Dasar Probability
& Counting
Apa itu Probability?
Probability adalah pengukuran terhadap suatu kemungkinan atau
peluang.
Pemahaman terkait probability
merupakan dasar untuk melangkah ke Statistika Inferensi (Inferential
Statistics).
Terminologi
●
Hasil dari
suatu percobaan (trial) dikenal sebagai outcome.
●
Himpunan dari
seluruh kemungkinan outcome pada suatu probability experiment dikenal sebagai sample
space.
●
Bagian dari
sample space dikenal sebagai event.
●
Event bisa
terdiri dari satu atau lebih outcomes.
Probability Experiments
Probability Experiments adalah aksi atau percobaan (trial) yang
menghasilkan suatu perhitungan, pengukuran, atau respon (counts,
measurements, or responses).
Probability Experiments: contoh
Tree Diagram
Tree Diagram digunakan untuk memberikan gambaran secara visual
terkait setiap outcome dari suatu probability experiment.
Tree Diagram: contoh
Event
●
Event umumnya
direpresentasikan dengan huruf kapital (uppercase letters), seperti A,
B, dan C.
●
Suatu event
yang terdiri dari sebuah outcome dikenal sebagai simple event.
Event: contoh
●
Event melempar
sebuah koin dan dadu enam sisi serta mendapatkan head dan 3 merupakan simple
event dan bisa direpresentasikan sebagai A = {H3}.
●
Sedangkan
event melempar sebuah koin dan dadu enam sisi serta mendapatkan head dan
bilangan genap bukan merupakan simple event karena memiliki 3 kemungkinan
outcomes; event ini bisa direpresentasikan sebagai B = {H2, H4, H6}.
Fundamental Counting Principle
●
Pemanfaatan
Tree Diagram untuk menghitung banyaknya outcome dari sejumlah event tidaklah
praktis.
●
Sebagai
alternatif, kita bisa memanfaatkan Fundamental Counting Principle untuk
mengetahui jumlah kemungkinan outcomes dari dua atau lebih event yang muncul
secara berurutan.
Fundamental Counting Principle:
contoh
Fundamental Counting Principle:
studi kasus
Types of Probability
●
Probability
dapat dituliskan dalam format pecahan, desimal, atau persentase.
●
Probability
untuk kemunculan event E dapat dituliskan sebagai P(E).
Terdapat 3 tipe probability:
●
Classical
(theoretical) Probability
●
Empirical
(statistical) Probability
●
Subjective
Probability
Classical (theoretical)
Probability
Classical Probability digunakan
ketika setiap outcome pada sample space memiliki peluang yang sama untuk
muncul.
Classical (theoretical)
Probability: contoh
Empirical (statistical)
Probability
Empirical (statistical)
Probability: contoh
Suatu perusahaan melakukan survey
online dengan memilih sejumlah responden secara acak untuk dimintai keterangan seberapa
sering mereka melakukan recycle. Sejauh ini mereka mendapatkan data dari 2,451
responden.
Law of Large Number
Ketika suatu probability
experiment dilakukan secara berulang-ulang, maka nilai empirical probability
yang dihasilkan akan mendekati nilai theoretical probability dari event
terkait.
Law of Large Number: simulasi
Subjective Probability
Subjective Probability didasarkan
pada intuisi, educated guesses, dan estimasi.
Contoh:
● Seorang dokter memberikan estimasi keberhasilan dari
proses operasi yang ditanganinya sebesar 90%.
● Seorang mahasiswa merasa yakin bahwa peluangnya untuk
lulus di matakuliah statistika adalah 70%.
Range of Probability
Probability dari suatu event E
akan memiliki jangkauan antara 0 sampai dengan 1.
Complementary Events
Complement dari event E adalah
semua oucomes pada sample space yang tidak disertakan pada event E; Complement
dari event E direpresentasikan sebagai
Complementary Events: contoh
Complementary Events: studi kasus
Probability: studi kasus

















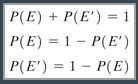











































.png)
